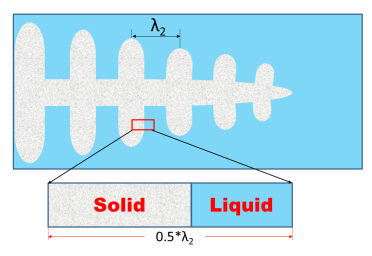
图 1所示为单个枝晶示意图，初生枝晶臂是一个较大的枝干，二次枝晶臂对称分布在两侧，二次枝晶臂间距(SDAS)表示为λ₂。通常使用二次枝晶臂之间区域内的一维形态来描述枝晶的凝固过程，由于枝晶臂的对称性，没有质量流过臂的中心，因此，仅考虑虑二次枝晶臂间距的一半0.5* λ₂，如图 1 底部显示的放大部分。

固相中的反向扩散

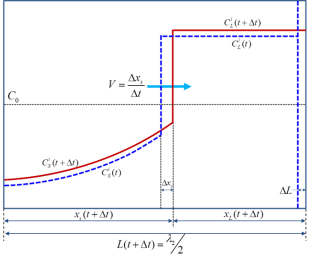
图 2所示为所考虑的枝晶臂中组分i的浓度变化曲线示意图。 和 分别是液相和固相中组元 i 的成分。V是固/液界面的推移速度。在时间间隔Δt期间，固/液界面前进Δx_s（由于凝固），同时凝固区域的长度增加ΔL（由于枝晶臂粗化）。对于每个时间步长内的瞬时凝固模拟，要执行三个主要任务：（1）计算固/液界面上每个组元的成分，考虑过冷效应和局部平衡条件；（2）求解固相内的扩散方程； （3）更新凝固区域的长度变量，以保证每个组元的质量平衡。一些经典教科书[1974Fle, 1985Kur] 中对反向扩散有更详细的描述。

(1)

其中V, ΔT₀, 分别是界面凝固速度，凝固温度范围和平衡分配系数。δ是与扰动谐波有关的常数。

模型中液相和固相中的扩散距离为枝晶臂间距。根据再熔化和再凝固的机制，枝晶臂的粗化对凝固过程中的均质化有很大影响，枝晶臂粗化的计算公式如下[1986Roo]：

(2)

其中， λ₀是初始二次枝晶臂间距，由枝晶尖端半径（方程 (1)）计算而得，λ是在指定时间的模型预测的二次枝晶臂间距。M是粗化参数，与 λ^1/3成正比；t 是时间；g 是几何因子，代表枝晶几何形状的影响。

对于二元体系，粗化参数M定义为 [1990Roo]：

(3)

对于多元体系，需要分别计算每个合金元素的粗化参数。然后，利用以下模型来计算所有溶质元素的总的粗化参数：

(4)

假设液/固界面处为局部平衡，通过PanEngine [2009Cao] ]可以直接计算出在每个时间步长，上述方程式中所需的所有与相平衡有关的量（例如m_L和k_e）。